Unidad Educativa Julio Verne
Fecha: 15 de mayo de 2020.
Tema: Reglas de tres simple directa e inversa.
Regla de tres simple directa.
La regla de tres simple directa se utiliza para resolver problemas que involucren magnitudes directamente proporcionales.
Ejemplo.
Por la compra de 14 lápices se paga 42 dólares. ¿Cuánto se pagará por 25 lápices?.
El proceso que seguimos en este caso es el mismo que aplicamos en la proporción directa, es decir buscamos el valor de x o de la incognita multiplicando los medios o extremos que conocemos y dividir para el término correspondiente ( medio o extemo).
Regla de tres inversa
La regla de tres inversa se utiliza para resolver problemas que involucren magnitudes inversamente proporcionales.
Ejemplo.-
Para trasportar una producción de arroz desde la hacienda a la ciudad se usan 3 camiones, estos deben realizar 6 viajes en total para llevar toda la carga, si hoy disponen solo de 2 camiones.¿Cuántos viajes serán necesarios?
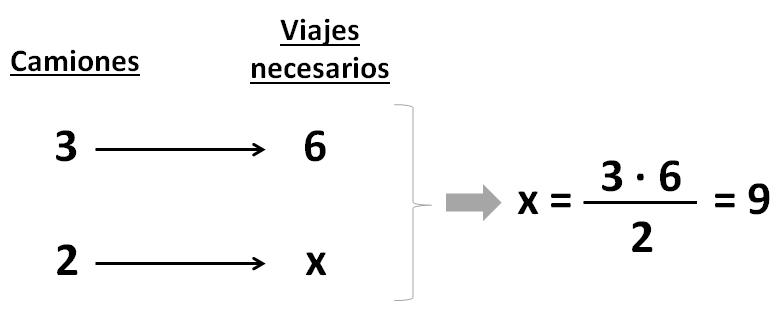
En este caso se aplica el proceso que usamos en proporción inversa, es decir identificamos los datos, ubicamos correctamente (camiones bajo camiones y viajes bajo viajes), luego multiplicamos de forma horizontal los términos que conocemos y dividimos para el término que se encuentra solo.
ACTIVIDAD
Revisar y trabajar las páginas 241, 243 , 244 y 245.
Proponer problemas para resolver con regla de tres directa e inversa.
TAREA
Realizar la siguiente actividad.
Porcentajes
El porcentaje permite comparar cantidades. Es una unidad de referencia que relaciona una magnitud con el todo que le corresponde. Se expresa con un número seguido del símbolo %. Una manera de calcular el porcentaje de una cantidad es multiplicar el número del porcentaje por la cantidad y luego dividir entre 100.
Ejemplo.-
Calcular el 15% de 5800.
Multiplico 15 por 5800 y se obtiene 87 000, este valor lo dividimos para 100, y su respuesta es 870.
Entonces podemos afirmar que el 15% de 5800 es 870.
Ejercicios.
Calcular el:
20% de 100
25% de 1000
12% de 450
7% de 170
70% de 1
ACTIVIDAD
Revisar y trabajar páginas 246, 247
DESCUENTOS Y AUMENTOS

Para calcular un descuento se sustrae o resta del precio inicial la cantidad correspondiente al porcentaje descontado.
Para calcular un aumento se adiciona al precio la cantidad correspondiente al porcentaje aumentado.
DESCUENTO= RESTO
AUMENTO= SUMO.
Ejemplo.
En el año 2013 hubo 1400 alumnos que seleccionaron la asignatura optativa de manualidades. En 2014 esta cifra bajó un 4%. ¿Cuántos alumnos la seleccionaron en 2014?
Para resolver este problema primero calculamos el 4% de 1400 que sería 56, es decir 56 estudiantes no eligieron la asignatura de manualidades en el 2014, pero la pregunta dice que cuantos estudiantes seleccionaron manualidades como asignatura optativa, entones restamos 56 a 1400 y tenemos 1344 estudiantes que si eligieron manualidades.
Operaciones realizadas:
4% de 1400 = 5600/100= 56
1400 - 56 = 1344.
RESOLVAMOS PROBLEMAS.
1.- Al adquirir un vehículo cuyo precio es de $ 8800 , nos hacen un descuento del 7.5%.
¿Cuánto hay que pagar por el vehículo?
¿Cuánto hay que pagar por el vehículo?
2.- El precio de un ordenador es de $ 1200 sin IVA. ¿Cuánto hay que pagar por él si el IVA es del 16%?
3.- Al comprar un monitor que cuesta $ 450 nos hacen un descuento del 8%.
¿Cuánto tenemos que pagar?
¿Cuánto tenemos que pagar?
4.- Se vende un artículo con una ganancia del 15% sobre el precio de costo.
Si se ha comprado en $ 80. Hallar el precio de venta.
Si se ha comprado en $ 80. Hallar el precio de venta.
MÁS ACTIVIDADES
Revisar y resolver páginas 248 y 249.
Profe. Jacky.



Comentarios
Publicar un comentario